En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia.

La característica esencial de un conjunto es la de estar bien definido, es decir que dado un objeto particular, determinar si este pertenece o no al conjunto. Por ejemplo si se considera el conjunto de los números dígitos, sabemos que el 3 pertenece al conjunto, pero el 19 no. Por otro lado el conjunto de las bellas obras musicales no es un conjunto bien definido, puesto que diferentes personas puedan incluir distintas obras en el conjunto.
Los objetos que forman un conjunto son llamados miembros o elementos. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:
El detallar a todos los elementos de un conjunto entre las llaves, se denomina forma tabular, extensión o enumeración de los elementos.
Dos conjuntos son iguales si tienen los mismos elementos, por ejemplo:
El conjunto { a, b, c } también puede escribirse:
{ a, c, b }, { b, a, c }, { b, c, a }, { c, a, b }, { c, b, a }
En teoría de conjuntos se acostumbra no repetir a los elementos por ejemplo:
El conjunto { b, b, b, d, d } simplemente será { b, d }.
Un elemento es... A los objetos que conforman los conjuntos los llamamos elementos.
Diagramas de Venn
Para representar los conjuntos gráficamente, se pueden usar los diagramas de Venn.
Este método consiste en representar los conjuntos por medio de círculos
y dibujar en su interior los elementos que lo conforman.
Por ejemplo, si el conjunto A está conformado por los elementos 1 , 2 y 3 podemos representarlo como se muestra en la figura.
Si dos o más conjuntos comparten elementos también es posible usar diagramas de Venn para representar esa situación.
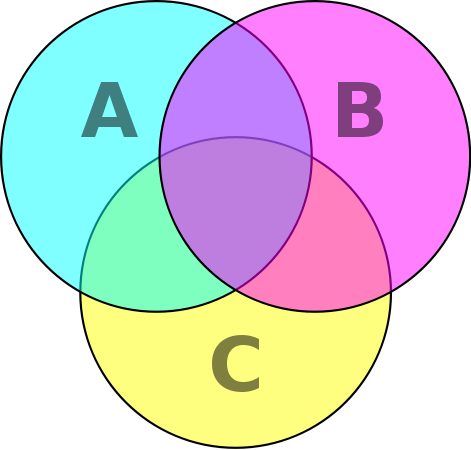
UNIVERSO O CONJUNTO UNIVERSAL
El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, se denota con la letra U y algunas veces con la letra S (espacio muestral).
Por ejemplo si solo queremos referirnos a los 5 primeros números naturales el conjunto queda:
U={ 1, 2, 3, 4, 5 }
Forma alternativa para indicar conjuntos de gran importancia:
N={ 1, 2, 3, .... }
Z={..., -2, -1, 0, 1, 2, ... }
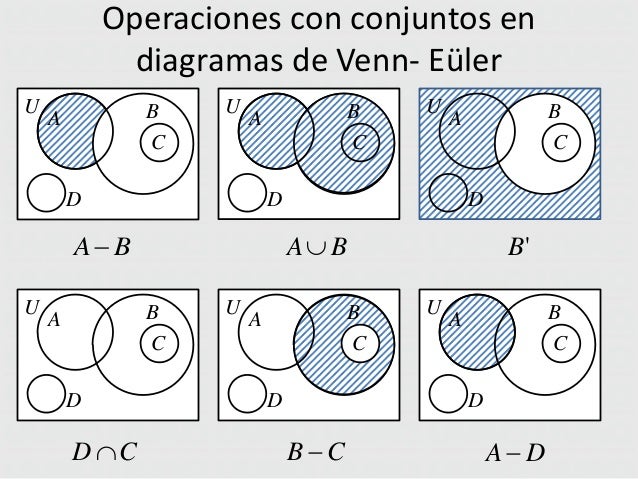
Si dos o más conjuntos comparten elementos también es posible usar diagramas de Venn para representar esa situación.

UNIVERSO O CONJUNTO UNIVERSAL
El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, se denota con la letra U y algunas veces con la letra S (espacio muestral).
Por ejemplo si solo queremos referirnos a los 5 primeros números naturales el conjunto queda:
Forma alternativa para indicar conjuntos de gran importancia:
- Conjunto de números naturales (enteros mayores que cero) representados por la letra N donde
- Conjunto de números enteros positivos y negativos representados por la letra Z donde
- Conjunto de números racionales (números que se representan como el cociente de dos números enteros {fracciones }). Estos números se representan por una Q
- Conjunto de números irracionales (números que no puedan representarse como el cociente de dos números enteros) representados por la letra I.
- Conjunto de los números reales que son los números racionales e irracionales es decir todos, representados por R.



0 comentarios :
Publicar un comentario