Isomorfismo

Esta característica significa construir modelos similares al modelo original, esto con el fin de aumentar o mejorar el desempeño de un sistema.

Dos grafos G₁ y G₂ son isomorfos si existe una función biyectiva f entre los vértices de G₁ y G₂, y una función biyectiva g entre lados de G₁ y G₂ tales que un lado e es incidente a v y w en G1 si solo si el lado g(e) es incidente a los vértices f (v) y f (w) en G₂. Al par de funciones f y g se le denomina isomorfismo.

Ejemplo:
Sean los siguientes grafos G₁ y G₂

 



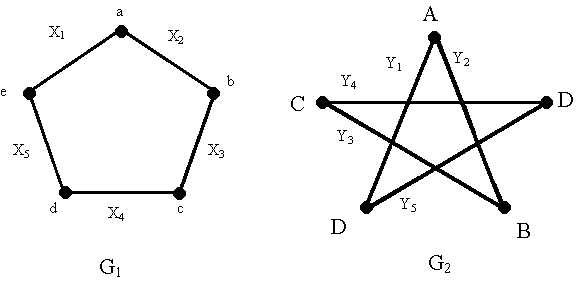
Un isomorfismo para los grafos anteriores G₁ y G₂ esta definido por:
f (a) = A
f (b) = B
f (c) = C
f (d) = D
f (e) = E

Los grafos G₁ y G₂ son isomorfos si y solo si para alguna ordenación de vértices y lados sus matrices de incidencia son iguales. Veamos las matrices de incidencia de los grafos anteriores:


 

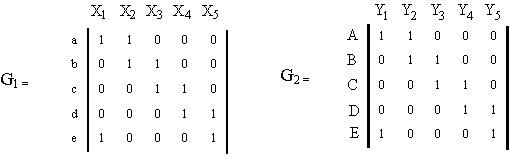
CARACTERIZACIÓN DE LOS GRAFOS

Un problema interesante en la teoría de grafos, que no ha sido resuelto del todo, es el referente a la búsqueda de todos los grafos simples diferentes que existen con un número determinado de vértices (caracterización de los grafos). Así, para p = 1 hay un solo grafo.

Así, para p = 1 hay un solo grafo

 

Para p = 2, existen dos grafos diferentes.

Para p = 3 ya llegan a ser cuatro grafos

 

.

Pero para p = 4 ya nos encontramos con once grafos distintos. 

 

 

 

Si hacemos esto para todos los grafos simples diferentes que existen con un número "p" de vértices, vemos que a medida que "p" crece el número de grafos aumenta considerablemente. 

 

Esto es un problema muy complejo, y para que se tenga una idea, cuando p = 9, existen 274668 grafos diferentes y conviene clasificar los grafos en ciertas familias de acuerdo a algunas propiedades específicas.

 

Arista

En teoría de grafos, una arista corresponde a una relación entre dos vértices de un grafo.

Para caracterizar un grafo G son suficientes únicamente el conjunto de todas sus aristas, comúnmente denotado con la letra E (del término en inglés edge), junto con el conjunto de sus vértices, denotado por V. Así, dicho grafo se puede representar como G(V,E), o bien G = (V,E).

En un grafo, dos vértices son adyacentes si están conectados por una arista. En tal caso, cada uno de estos vértices es incidente a dicha arista.

No es obligatorio que todo vértice esté unido con otro por una arista. Tales vértices se llaman vértices o nodos aislados
 

 

Vértice

En teoría de grafos, un vértice o nodo es la unidad fundamental de la que están formados los grafos. Un grafo no dirigido está formado por un conjunto de vértices y un conjunto de aristas (pares no ordenados de vértices), mientras que un grafo dirigido está compuesto por un conjunto de vértices y un conjunto de arcos (pares ordenados de vértices). En este contexto, los vértices son tratados como objetos indivisibles y sin propiedades, aunque puedan tener una estructura adicional dependiendo de la aplicación por la cual se usa el grafo; por ejemplo, una red semántica es un grafo en donde los vértices representan conceptos o clases de objetos.

 

Grado

El grado de un vértice en un grafo es el número de aristas incidentes a él. Un vértice aislado es un vértice con grado cero; esto es, un vértice que no es punto final de ninguna arista.